Pöschl-Teller Potential

The Pöschl-Teller potential is one of the few potentials for which the quantum mechanical Schrödinger equation has an analytical solution. It has a finite number of bound states, which can be inferred easily from its potential strength parameter λ. It is defined for one-dimensional systems.

Definitions

Antique.PoschlTeller — Type

Model

This model is described with the time-independent Schrödinger equation

\[ \hat{H} \psi(x) = E \psi(x),\]

and the Hamiltonian

\[ \hat{H} = - \frac{\hbar^2}{2 m} \frac{\mathrm{d}^2}{\mathrm{d}x ^2} - \frac{\hbar^2}{m x_0^2} \frac{\lambda(\lambda+1)}{2} \frac{1}{\mathrm{cosh}^2(x/x_0)}.\]

After introducing the dimensionless variables

\[ x^\ast \equiv x/x_0,\qquad E^\ast \equiv \frac{\hbar^2}{m x_0^2} E\]

the Schrödinger equation reduces to

\[ \hat{H}^\ast \psi(x^\ast) = E^\ast \psi(x^\ast),\]

with

\[ \hat{H}^\ast = - \frac{1}{2} \frac{\mathrm{d}^2}{\mathrm{d}{x^\ast}^2} - \frac{\lambda(\lambda+1)}{2} \frac{1}{\mathrm{cosh}^2(x^\ast)}.\]

Parameters are specified within the following struct:

PT = PoschlTeller(λ=1, m=1.0, ℏ=1.0, x₀=1.0)

$\lambda$ determines the potential strength. Currently only integer values for $\lambda$ are supported.

References

G. Pöschl, E. Teller, Zeitschrift für Physik, 83 (3–4), 143 (1933): More general definitions are given as (2a), (2b) or (11).
S. Flügge, Practical Quantum Mechanics (Springer Berlin Heidelberg, 1999) p.94 Problem 39. Potential hole of modified Poschl-Teller type.

source

Potential

Antique.V — Method

V(model::PoschlTeller, x)

\[\begin{aligned} V(x) &= -\frac{\hbar^2}{m x_0^2} \frac{\lambda(\lambda+1)}{2} \mathrm{sech}^2(x/x_0) \\ &= -\frac{\hbar^2}{m x_0^2} \frac{\lambda(\lambda+1)}{2} \frac{1}{\mathrm{cosh}^2(x/x_0)} . \end{aligned}\]

source

Maximum Quantum Number

Antique.nₘₐₓ — Method

nₘₐₓ(model::PoschlTeller)

Note

Note that the number of bound states nₘₐₓ + 1 is not equal to the maximum quantum number nₘₐₓ, since we count the ground state from n=0 in this model.

\[n_\mathrm{max} = \left\lfloor \lambda \right\rfloor - 1.\]

source

Eigenvalues

Antique.E — Method

E(model::PoschlTeller; n::Int=0, nocheck=false)

\[E_n = -\frac{\hbar^2}{m x_0^2}\frac{\mu^2}{2},\]

where $\mu = \mu(n) = n_\mathrm{max}-n+1$, and $n_\mathrm{max} = \left\lfloor \lambda \right\rfloor - 1$.

source

Eigenfunctions

Antique.ψ — Method

ψ(model::PoschlTeller, x; n::Int=0)

\[\psi_n(x) = \frac{(-1)^μ}{\sqrt{x_0}} P_\lambda^{\mu}(\mathrm{tanh}(x/x_0)) \sqrt{\mu\frac{\Gamma(\lambda-\mu+1)}{\Gamma(\lambda+\mu+1)}},\]

where $\mu = \mu(n) = n_\mathrm{max}-n+1$, and $n_\mathrm{max} = \left\lfloor \lambda \right\rfloor - 1$ and $P_\lambda^{\mu}$ are the associated Legendre functions.

source

Associated Legendre Polynomials

Antique.P — Method

P(model::PoschlTeller, x; n=0, m=0)

Associated Legendre polynomials are the associated Legendre functions for integer indices. Here we use the same notation of the associated Legendre functions as in the model HydrogenAtom.

\[\begin{aligned} P_n^m(x) &= \left( 1-x^2 \right)^{m/2} \frac{\mathrm{d}^m}{\mathrm{d}x^m} P_n(x) \\ &= \left( 1-x^2 \right)^{m/2} \frac{\mathrm{d}^m}{\mathrm{d}x^m} \frac{1}{2^n n!} \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left[ \left( x^2-1 \right)^n \right] \\ &= \frac{1}{2^n} (1-x^2)^{m/2} \sum_{j=0}^{\left\lfloor\frac{n-m}{2}\right\rfloor} (-1)^j \frac{(2n-2j)!}{j! (n-j)! (n-2j-m)!} x^{(n-2j-m)}. \end{aligned}\]

source

Usage & Examples

Install Antique.jl for the first use and run using Antique before each use. The energy E(), wavefunction ψ(), potential V() and nₘₐₓ() will be exported. In this system, the model is generated by PoschlTeller and the parameters λ, m, ℏ, x₀.

using Antique
PT = PoschlTeller(λ=4, m=1.0, ℏ=1.0, x₀=1.0)

Parameters:

julia> PT.λ4
julia> PT.m1.0
julia> PT.ℏ1.0
julia> PT.x₀1.0

Maximum quantum number:

julia> nₘₐₓ(PT)3

Eigenvalues:

julia> E(PT, n=0)-8.0
julia> E(PT, n=1)-4.5
julia> E(PT, n=2)-2.0
julia> E(PT, n=3)-0.5

Potential energy curve:

using CairoMakie

f = Figure()
ax = Axis(f[1,1], xlabel=L"$x$", ylabel=L"$V(x)$")
lines!(ax, -6..6, x -> V(PT, x))
f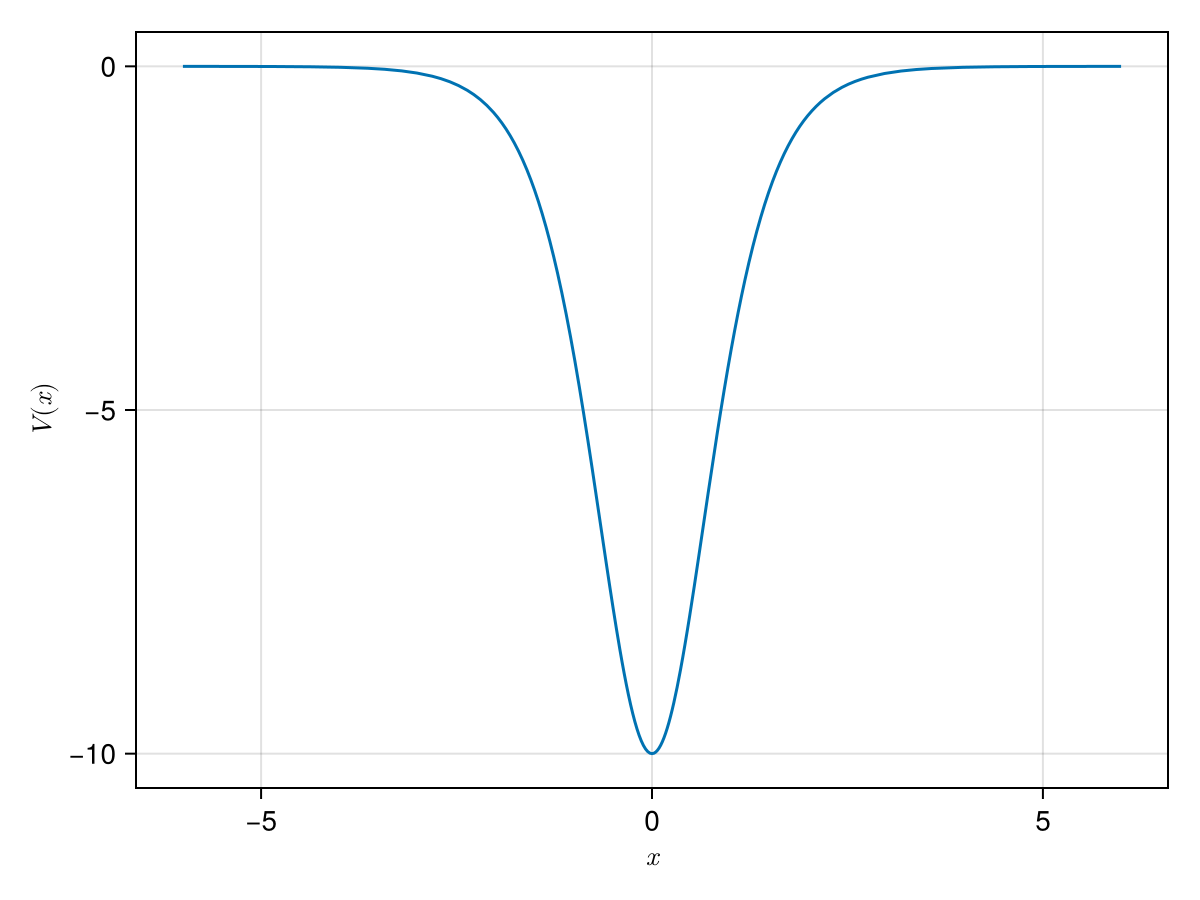

Wave functions:

using CairoMakie

# setting
f = Figure()
ax = Axis(f[1,1], xlabel=L"$x$", ylabel=L"$\psi(x)$")

# plot
w0 = lines!(ax, -3..3, x -> ψ(PT, x, n=0))
w1 = lines!(ax, -3..3, x -> ψ(PT, x, n=1))
w2 = lines!(ax, -3..3, x -> ψ(PT, x, n=2))
w3 = lines!(ax, -3..3, x -> ψ(PT, x, n=3))

# legend
axislegend(ax, [w0, w1, w2, w3], [L"n=0", L"n=1", L"n=2", L"n=3"], position=:lb)

f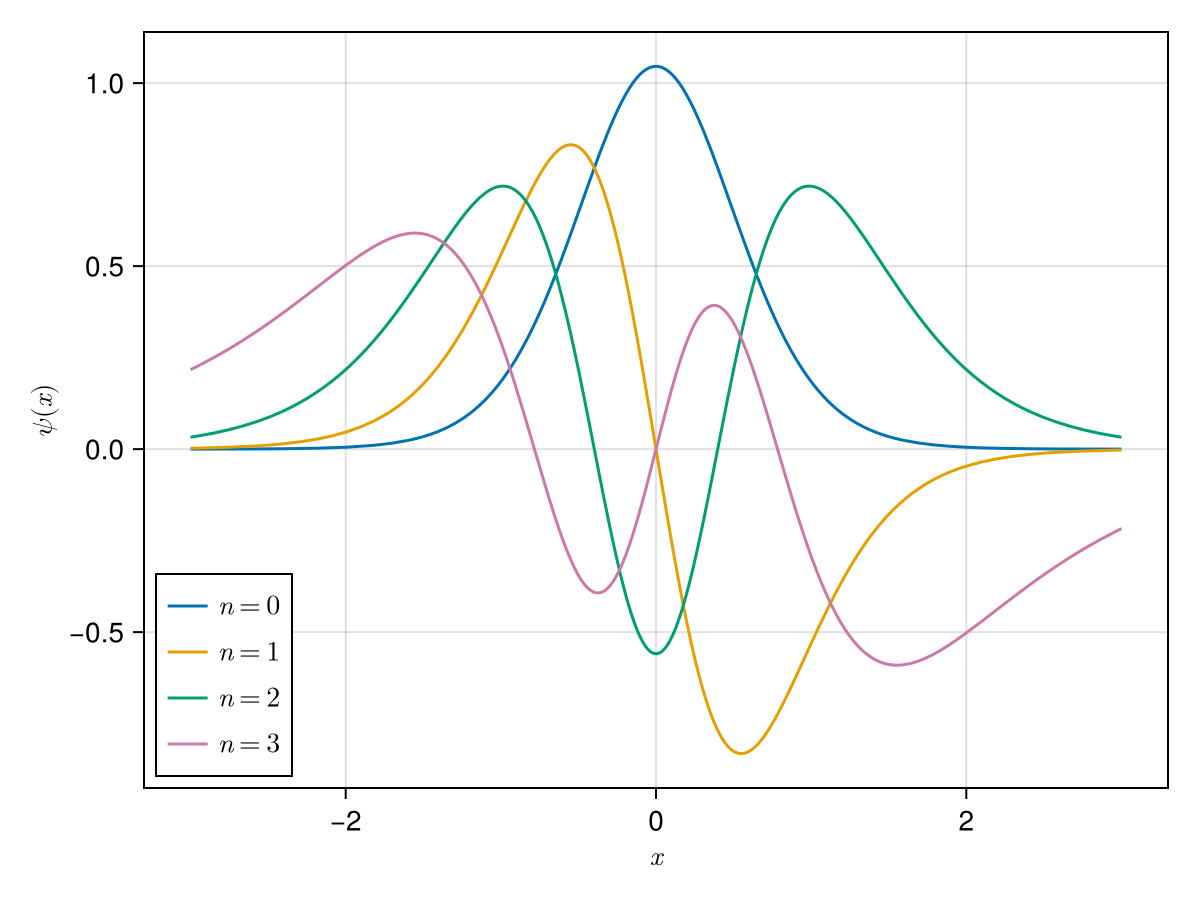

Potential energy curve, Energy levels, Wave functions:

using CairoMakie

# settings
f = Figure()
ax = Axis(f[1,1], xlabel=L"$x$", ylabel=L"$V(x),~E_n,~\psi_n(x) \times 5 + E_n$", aspect=1, limits=(-4,4,-10.5,1))
# hidespines!(ax)
# hidedecorations!(ax)

for n in 0:3
  # classical turning point
  xE = acosh(sqrt(PT.λ*(PT.λ+1)/abs(E(PT,n=n))/2))
  # energy
  hlines!(ax, E(PT, n=n), color=:black, linewidth=1, linestyle=:dash)
  lines!(ax, [-xE,xE], fill(E(PT,n=n),2), color=:black, linewidth=2)
  # wave function
  lines!(ax, -4..4, x -> E(PT,n=n) + ψ(PT,x,n=n), linewidth=2)
end

#potential
lines!(ax, -4..4, x -> V(PT,x), color=:black, linewidth=2)

f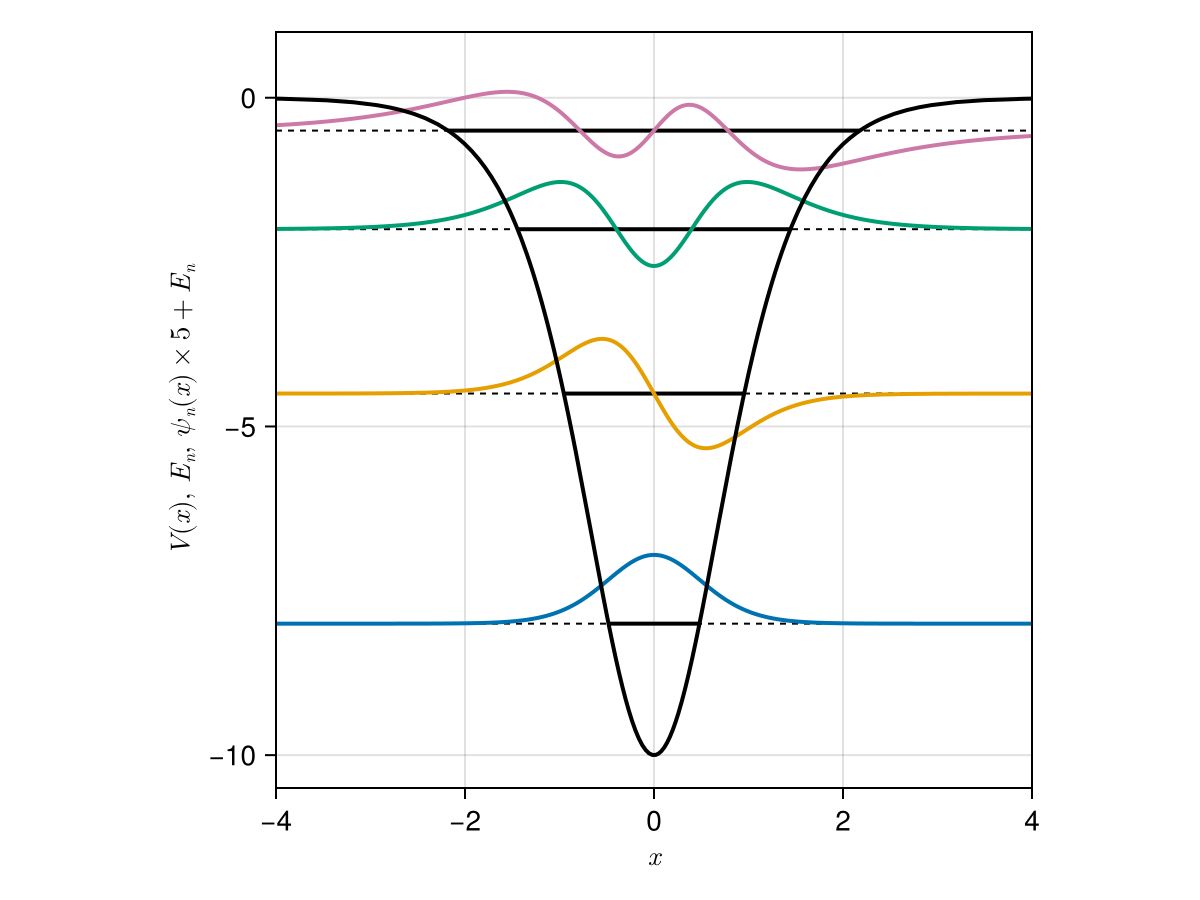

Testing

Unit testing and Integration testing were done using numerical integration (QuadGK.jl). The test script is here.

Associated Legendre Polynomials $P_n^m(x)$

\[ \begin{aligned} P_n^m(x) &= \left( 1-x^2 \right)^{m/2} \frac{\mathrm{d}^m}{\mathrm{d}x^m} P_n(x) \\ &= \left( 1-x^2 \right)^{m/2} \frac{\mathrm{d}^m}{\mathrm{d}x^m} \frac{1}{2^n n!} \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left[ \left( x^2-1 \right)^n \right] \\ &= \frac{1}{2^n} (1-x^2)^{m/2} \sum_{j=0}^{\left\lfloor\frac{n-m}{2}\right\rfloor} (-1)^j \frac{(2n-2j)!}{j! (n-j)! (n-2j-m)!} x^{(n-2j-m)}. \end{aligned}\]

$n=0, m=0:$ ✔

\[\begin{aligned} P_{0}^{0}(x) = 1 &= 1 \\ &= 1 \end{aligned}\]

$n=1, m=0:$ ✔

\[\begin{aligned} P_{1}^{0}(x) = \frac{1}{2} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right) &= x \\ &= x \end{aligned}\]

$n=1, m=1:$ ✔

\[\begin{aligned} P_{1}^{1}(x) = \left( 1 - x^{2} \right)^{\frac{1}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{2} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right) &= \left( 1 - x^{2} \right)^{\frac{1}{2}} \\ &= \left( 1 - x^{2} \right)^{\frac{1}{2}} \end{aligned}\]

$n=2, m=0:$ ✔

\[\begin{aligned} P_{2}^{0}(x) = \frac{1}{8} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{2} &= \frac{-1}{2} + \frac{3}{2} x^{2} \\ &= \frac{-1}{2} + \frac{3}{2} x^{2} \end{aligned}\]

$n=2, m=1:$ ✔

\[\begin{aligned} P_{2}^{1}(x) = \left( 1 - x^{2} \right)^{\frac{1}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{8} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{2} &= 3 \left( 1 - x^{2} \right)^{\frac{1}{2}} x \\ &= 3 \left( 1 - x^{2} \right)^{\frac{1}{2}} x \end{aligned}\]

$n=2, m=2:$ ✔

\[\begin{aligned} P_{2}^{2}(x) = \left( 1 - x^{2} \right) \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{8} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{2} &= 3 - 3 x^{2} \\ &= 3 - 3 x^{2} \end{aligned}\]

$n=3, m=0:$ ✔

\[\begin{aligned} P_{3}^{0}(x) = \frac{1}{48} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{3} &= - \frac{3}{2} x + \frac{5}{2} x^{3} \\ &= - \frac{3}{2} x + \frac{5}{2} x^{3} \end{aligned}\]

$n=3, m=1:$ ✔

\[\begin{aligned} P_{3}^{1}(x) = \left( 1 - x^{2} \right)^{\frac{1}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{48} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{3} &= - \frac{3}{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} + \frac{15}{2} x^{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} \\ &= - \frac{3}{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} + \frac{15}{2} x^{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} \end{aligned}\]

$n=3, m=2:$ ✔

\[\begin{aligned} P_{3}^{2}(x) = \left( 1 - x^{2} \right) \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{48} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{3} &= 15 x - 15 x^{3} \\ &= 15 x - 15 x^{3} \end{aligned}\]

$n=3, m=3:$ ✔

\[\begin{aligned} P_{3}^{3}(x) = \left( 1 - x^{2} \right)^{\frac{3}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{48} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{3} &= 15 \left( 1 - x^{2} \right)^{\frac{3}{2}} \\ &= 15 \left( 1 - x^{2} \right)^{\frac{3}{2}} \end{aligned}\]

$n=4, m=0:$ ✔

\[\begin{aligned} P_{4}^{0}(x) = \frac{1}{384} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{4} &= \frac{3}{8} - \frac{15}{4} x^{2} + \frac{35}{8} x^{4} \\ &= \frac{3}{8} - \frac{15}{4} x^{2} + \frac{35}{8} x^{4} \end{aligned}\]

$n=4, m=1:$ ✔

\[\begin{aligned} P_{4}^{1}(x) = \left( 1 - x^{2} \right)^{\frac{1}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{384} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{4} &= - \frac{15}{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} x + \frac{35}{2} x^{3} \left( 1 - x^{2} \right)^{\frac{1}{2}} \\ &= - \frac{15}{2} \left( 1 - x^{2} \right)^{\frac{1}{2}} x + \frac{35}{2} x^{3} \left( 1 - x^{2} \right)^{\frac{1}{2}} \end{aligned}\]

$n=4, m=2:$ ✔

\[\begin{aligned} P_{4}^{2}(x) = \left( 1 - x^{2} \right) \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{384} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{4} &= \frac{-15}{2} + 60 x^{2} - \frac{105}{2} x^{4} \\ &= \frac{-15}{2} + 60 x^{2} - \frac{105}{2} x^{4} \end{aligned}\]

$n=4, m=3:$ ✔

\[\begin{aligned} P_{4}^{3}(x) = \left( 1 - x^{2} \right)^{\frac{3}{2}} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{384} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{4} &= 105 \left( 1 - x^{2} \right)^{\frac{3}{2}} x \\ &= 105 \left( 1 - x^{2} \right)^{\frac{3}{2}} x \end{aligned}\]

$n=4, m=4:$ ✔

\[\begin{aligned} P_{4}^{4}(x) = \left( 1 - x^{2} \right)^{2} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{1}{384} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\mathrm{d}}{\mathrm{d}x} \left( -1 + x^{2} \right)^{4} &= 105 \left( 1 - x^{2} \right)^{2} \\ &= 105 \left( 1 - x^{2} \right)^{2} \end{aligned}\]

Normalization & Orthogonality of $\psi_n(x)$

\[\int \psi_i^\ast(x) \psi_j(x) \mathrm{d}x = \delta_{ij}\]

  λ |   m |   ℏ |  x₀ |  i |  j |     analytical |      numerical 
--- | --- | --- | --- | -- | -- | -------------- | -------------- 
1.0 | 1.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 1.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
1.0 | 2.7 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 1.0 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 1.0 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 1.0 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.0 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.0 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.0 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
2.0 | 2.7 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
2.0 | 2.7 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
2.0 | 2.7 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 1.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 1.0 | 2.7 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 1.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.0 | 2.7 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 1.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.0 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 1.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  0 |  1 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  0 |  2 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  1 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  2 |  0 |    0.000000000 |   -0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.0 |  2 |  2 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  0 |  0 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  0 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  0 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  1 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  1 |  1 |    1.000000000 |    1.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  1 |  2 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  2 |  0 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  2 |  1 |    0.000000000 |    0.000000000 ✔
3.0 | 2.7 | 2.7 | 2.7 |  2 |  2 |    1.000000000 |    1.000000000 ✔

Eigenvalues

\[ \begin{aligned} E_n &= \int \psi^\ast_n(x) \hat{H} \psi_n(x) \mathrm{d}x \\ &= \int \psi^\ast_n(x) \left[ \hat{V} + \hat{T} \right] \psi(x) \mathrm{d}x \\ &= \int \psi^\ast_n(x) \left[ V(x) - \frac{\hbar^2}{2m} \frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} \right] \psi(x) \mathrm{d}x \\ &\simeq \int \psi^\ast_n(x) \left[ V(x)\psi(x) -\frac{\hbar^2}{2m} \frac{\psi(x+\Delta x) - 2\psi(x) + \psi(x-\Delta x)}{\Delta x^{2}} \right] \mathrm{d}x. \end{aligned}\]

Where, the difference formula for the 2nd-order derivative:

\[\begin{aligned} % 2\psi(x) % + \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} \Delta x^{2} % + O\left(\Delta x^{4}\right) % &= % \psi(x+\Delta x) % + \psi(x-\Delta x) % \\ % \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} \Delta x^{2} % &= % \psi(x+\Delta x) % - 2\psi(x) % + \psi(x-\Delta x) % - O\left(\Delta x^{4}\right) % \\ % \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} % &= % \frac{\psi(x+\Delta x) - 2\psi(x) + \psi(x-\Delta x)}{\Delta x^{2}} % - \frac{O\left(\Delta x^{4}\right)}{\Delta x^{2}} % \\ \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} &= \frac{\psi(x+\Delta x) - 2\psi(x) + \psi(x-\Delta x)}{\Delta x^{2}} + O\left(\Delta x^{2}\right) \end{aligned}\]

are given by the sum of 2 Taylor series:

\[\begin{aligned} \psi(x+\Delta x) &= \psi(x) + \frac{\mathrm{d} \psi(x)}{\mathrm{d} x} \Delta x + \frac{1}{2!} \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} \Delta x^{2} + \frac{1}{3!} \frac{\mathrm{d}^{3} \psi(x)}{\mathrm{d} x^{3}} \Delta x^{3} + O\left(\Delta x^{4}\right), \\ \psi(x-\Delta x) &= \psi(x) - \frac{\mathrm{d} \psi(x)}{\mathrm{d} x} \Delta x + \frac{1}{2!} \frac{\mathrm{d}^{2} \psi(x)}{\mathrm{d} x^{2}} \Delta x^{2} - \frac{1}{3!} \frac{\mathrm{d}^{3} \psi(x)}{\mathrm{d} x^{3}} \Delta x^{3} + O\left(\Delta x^{4}\right). \end{aligned}\]

  λ |   m |   ℏ |  x₀ |  n |     analytical |      numerical 
--- | --- | --- | --- | -- | -------------- | -------------- 
1.0 | 1.0 | 1.0 | 1.0 |  0 |   -0.500000000 |   -0.500000019 ✔
1.0 | 1.0 | 1.0 | 2.0 |  0 |   -0.125000000 |   -0.124999975 ✔
1.0 | 1.0 | 1.0 | 2.7 |  0 |   -0.067667642 |   -0.067667643 ✔
1.0 | 1.0 | 2.0 | 1.0 |  0 |   -2.000000000 |   -2.000000077 ✔
1.0 | 1.0 | 2.0 | 2.0 |  0 |   -0.500000000 |   -0.500000002 ✔
1.0 | 1.0 | 2.0 | 2.7 |  0 |   -0.270670566 |   -0.270670571 ✔
1.0 | 1.0 | 2.7 | 1.0 |  0 |   -3.694528049 |   -3.694528192 ✔
1.0 | 1.0 | 2.7 | 2.0 |  0 |   -0.923632012 |   -0.923632016 ✔
1.0 | 1.0 | 2.7 | 2.7 |  0 |   -0.500000000 |   -0.500000008 ✔
1.0 | 2.0 | 1.0 | 1.0 |  0 |   -0.250000000 |   -0.250000010 ✔
1.0 | 2.0 | 1.0 | 2.0 |  0 |   -0.062500000 |   -0.062499987 ✔
1.0 | 2.0 | 1.0 | 2.7 |  0 |   -0.033833821 |   -0.033833845 ✔
1.0 | 2.0 | 2.0 | 1.0 |  0 |   -1.000000000 |   -1.000000038 ✔
1.0 | 2.0 | 2.0 | 2.0 |  0 |   -0.250000000 |   -0.249999975 ✔
1.0 | 2.0 | 2.0 | 2.7 |  0 |   -0.135335283 |   -0.135335285 ✔
1.0 | 2.0 | 2.7 | 1.0 |  0 |   -1.847264025 |   -1.847264096 ✔
1.0 | 2.0 | 2.7 | 2.0 |  0 |   -0.461816006 |   -0.461816008 ✔
1.0 | 2.0 | 2.7 | 2.7 |  0 |   -0.250000000 |   -0.250000004 ✔
1.0 | 2.7 | 1.0 | 1.0 |  0 |   -0.183939721 |   -0.183939703 ✔
1.0 | 2.7 | 1.0 | 2.0 |  0 |   -0.045984930 |   -0.045984921 ✔
1.0 | 2.7 | 1.0 | 2.7 |  0 |   -0.024893534 |   -0.024893552 ✔
1.0 | 2.7 | 2.0 | 1.0 |  0 |   -0.735758882 |   -0.735758911 ✔
1.0 | 2.7 | 2.0 | 2.0 |  0 |   -0.183939721 |   -0.183939702 ✔
1.0 | 2.7 | 2.0 | 2.7 |  0 |   -0.099574137 |   -0.099574138 ✔
1.0 | 2.7 | 2.7 | 1.0 |  0 |   -1.359140914 |   -1.359140966 ✔
1.0 | 2.7 | 2.7 | 2.0 |  0 |   -0.339785229 |   -0.339785230 ✔
1.0 | 2.7 | 2.7 | 2.7 |  0 |   -0.183939721 |   -0.183939723 ✔
2.0 | 1.0 | 1.0 | 1.0 |  0 |   -2.000000000 |   -2.000000095 ✔
2.0 | 1.0 | 1.0 | 1.0 |  1 |   -0.500000000 |   -0.500000184 ✔
2.0 | 1.0 | 1.0 | 2.0 |  0 |   -0.500000000 |   -0.500000005 ✔
2.0 | 1.0 | 1.0 | 2.0 |  1 |   -0.125000000 |   -0.125000010 ✔
2.0 | 1.0 | 1.0 | 2.7 |  0 |   -0.270670566 |   -0.270670578 ✔
2.0 | 1.0 | 1.0 | 2.7 |  1 |   -0.067667642 |   -0.067667647 ✔
2.0 | 1.0 | 2.0 | 1.0 |  0 |   -8.000000000 |   -8.000000381 ✔
2.0 | 1.0 | 2.0 | 1.0 |  1 |   -2.000000000 |   -2.000000736 ✔
2.0 | 1.0 | 2.0 | 2.0 |  0 |   -2.000000000 |   -2.000000024 ✔
2.0 | 1.0 | 2.0 | 2.0 |  1 |   -0.500000000 |   -0.500000038 ✔
2.0 | 1.0 | 2.0 | 2.7 |  0 |   -1.082682266 |   -1.082682311 ✔
2.0 | 1.0 | 2.0 | 2.7 |  1 |   -0.270670566 |   -0.270670588 ✔
2.0 | 1.0 | 2.7 | 1.0 |  0 |  -14.778112198 |  -14.778112902 ✔
2.0 | 1.0 | 2.7 | 1.0 |  1 |   -3.694528049 |   -3.694529413 ✔
2.0 | 1.0 | 2.7 | 2.0 |  0 |   -3.694528049 |   -3.694528093 ✔
2.0 | 1.0 | 2.7 | 2.0 |  1 |   -0.923632012 |   -0.923632083 ✔
2.0 | 1.0 | 2.7 | 2.7 |  0 |   -2.000000000 |   -2.000000083 ✔
2.0 | 1.0 | 2.7 | 2.7 |  1 |   -0.500000000 |   -0.500000041 ✔
2.0 | 2.0 | 1.0 | 1.0 |  0 |   -1.000000000 |   -1.000000047 ✔
2.0 | 2.0 | 1.0 | 1.0 |  1 |   -0.250000000 |   -0.250000092 ✔
2.0 | 2.0 | 1.0 | 2.0 |  0 |   -0.250000000 |   -0.250000003 ✔
2.0 | 2.0 | 1.0 | 2.0 |  1 |   -0.062500000 |   -0.062499986 ✔
2.0 | 2.0 | 1.0 | 2.7 |  0 |   -0.135335283 |   -0.135335289 ✔
2.0 | 2.0 | 1.0 | 2.7 |  1 |   -0.033833821 |   -0.033833824 ✔
2.0 | 2.0 | 2.0 | 1.0 |  0 |   -4.000000000 |   -4.000000191 ✔
2.0 | 2.0 | 2.0 | 1.0 |  1 |   -1.000000000 |   -1.000000367 ✔
2.0 | 2.0 | 2.0 | 2.0 |  0 |   -1.000000000 |   -1.000000011 ✔
2.0 | 2.0 | 2.0 | 2.0 |  1 |   -0.250000000 |   -0.250000019 ✔
2.0 | 2.0 | 2.0 | 2.7 |  0 |   -0.541341133 |   -0.541341155 ✔
2.0 | 2.0 | 2.0 | 2.7 |  1 |   -0.135335283 |   -0.135335294 ✔
2.0 | 2.0 | 2.7 | 1.0 |  0 |   -7.389056099 |   -7.389056451 ✔
2.0 | 2.0 | 2.7 | 1.0 |  1 |   -1.847264025 |   -1.847264705 ✔
2.0 | 2.0 | 2.7 | 2.0 |  0 |   -1.847264025 |   -1.847264047 ✔
2.0 | 2.0 | 2.7 | 2.0 |  1 |   -0.461816006 |   -0.461816041 ✔
2.0 | 2.0 | 2.7 | 2.7 |  0 |   -1.000000000 |   -1.000000042 ✔
2.0 | 2.0 | 2.7 | 2.7 |  1 |   -0.250000000 |   -0.250000020 ✔
2.0 | 2.7 | 1.0 | 1.0 |  0 |   -0.735758882 |   -0.735758917 ✔
2.0 | 2.7 | 1.0 | 1.0 |  1 |   -0.183939721 |   -0.183939788 ✔
2.0 | 2.7 | 1.0 | 2.0 |  0 |   -0.183939721 |   -0.183939723 ✔
2.0 | 2.7 | 1.0 | 2.0 |  1 |   -0.045984930 |   -0.045984920 ✔
2.0 | 2.7 | 1.0 | 2.7 |  0 |   -0.099574137 |   -0.099574141 ✔
2.0 | 2.7 | 1.0 | 2.7 |  1 |   -0.024893534 |   -0.024893536 ✔
2.0 | 2.7 | 2.0 | 1.0 |  0 |   -2.943035529 |   -2.943035670 ✔
2.0 | 2.7 | 2.0 | 1.0 |  1 |   -0.735758882 |   -0.735759152 ✔
2.0 | 2.7 | 2.0 | 2.0 |  0 |   -0.735758882 |   -0.735758890 ✔
2.0 | 2.7 | 2.0 | 2.0 |  1 |   -0.183939721 |   -0.183939735 ✔
2.0 | 2.7 | 2.0 | 2.7 |  0 |   -0.398296547 |   -0.398296564 ✔
2.0 | 2.7 | 2.0 | 2.7 |  1 |   -0.099574137 |   -0.099574145 ✔
2.0 | 2.7 | 2.7 | 1.0 |  0 |   -5.436563657 |   -5.436563916 ✔
2.0 | 2.7 | 2.7 | 1.0 |  1 |   -1.359140914 |   -1.359141414 ✔
2.0 | 2.7 | 2.7 | 2.0 |  0 |   -1.359140914 |   -1.359140930 ✔
2.0 | 2.7 | 2.7 | 2.0 |  1 |   -0.339785229 |   -0.339785254 ✔
2.0 | 2.7 | 2.7 | 2.7 |  0 |   -0.735758882 |   -0.735758913 ✔
2.0 | 2.7 | 2.7 | 2.7 |  1 |   -0.183939721 |   -0.183939736 ✔
3.0 | 1.0 | 1.0 | 1.0 |  0 |   -4.500000000 |   -4.500000232 ✔
3.0 | 1.0 | 1.0 | 1.0 |  1 |   -2.000000000 |   -2.000000667 ✔
3.0 | 1.0 | 1.0 | 1.0 |  2 |   -0.500000000 |   -0.500000668 ✔
3.0 | 1.0 | 1.0 | 2.0 |  0 |   -1.125000000 |   -1.125000014 ✔
3.0 | 1.0 | 1.0 | 2.0 |  1 |   -0.500000000 |   -0.500000042 ✔
3.0 | 1.0 | 1.0 | 2.0 |  2 |   -0.125000000 |   -0.125000038 ✔
3.0 | 1.0 | 1.0 | 2.7 |  0 |   -0.609008775 |   -0.609008780 ✔
3.0 | 1.0 | 1.0 | 2.7 |  1 |   -0.270670566 |   -0.270670599 ✔
3.0 | 1.0 | 1.0 | 2.7 |  2 |   -0.067667642 |   -0.067667658 ✔
3.0 | 1.0 | 2.0 | 1.0 |  0 |  -18.000000000 |  -18.000000929 ✔
3.0 | 1.0 | 2.0 | 1.0 |  1 |   -8.000000000 |   -8.000002667 ✔
3.0 | 1.0 | 2.0 | 1.0 |  2 |   -2.000000000 |   -2.000002680 ✔
3.0 | 1.0 | 2.0 | 2.0 |  0 |   -4.500000000 |   -4.500000058 ✔
3.0 | 1.0 | 2.0 | 2.0 |  1 |   -2.000000000 |   -2.000000167 ✔
3.0 | 1.0 | 2.0 | 2.0 |  2 |   -0.500000000 |   -0.500000151 ✔
3.0 | 1.0 | 2.0 | 2.7 |  0 |   -2.436035098 |   -2.436035115 ✔
3.0 | 1.0 | 2.0 | 2.7 |  1 |   -1.082682266 |   -1.082682315 ✔
3.0 | 1.0 | 2.0 | 2.7 |  2 |   -0.270670566 |   -0.270670632 ✔
3.0 | 1.0 | 2.7 | 1.0 |  0 |  -33.250752445 |  -33.250754161 ✔
3.0 | 1.0 | 2.7 | 1.0 |  1 |  -14.778112198 |  -14.778117124 ✔
3.0 | 1.0 | 2.7 | 1.0 |  2 |   -3.694528049 |   -3.694533001 ✔
3.0 | 1.0 | 2.7 | 2.0 |  0 |   -8.312688111 |   -8.312688219 ✔
3.0 | 1.0 | 2.7 | 2.0 |  1 |   -3.694528049 |   -3.694528358 ✔
3.0 | 1.0 | 2.7 | 2.0 |  2 |   -0.923632012 |   -0.923632314 ✔
3.0 | 1.0 | 2.7 | 2.7 |  0 |   -4.500000000 |   -4.500000031 ✔
3.0 | 1.0 | 2.7 | 2.7 |  1 |   -2.000000000 |   -2.000000090 ✔
3.0 | 1.0 | 2.7 | 2.7 |  2 |   -0.500000000 |   -0.500000122 ✔
3.0 | 2.0 | 1.0 | 1.0 |  0 |   -2.250000000 |   -2.250000116 ✔
3.0 | 2.0 | 1.0 | 1.0 |  1 |   -1.000000000 |   -1.000000333 ✔
3.0 | 2.0 | 1.0 | 1.0 |  2 |   -0.250000000 |   -0.250000334 ✔
3.0 | 2.0 | 1.0 | 2.0 |  0 |   -0.562500000 |   -0.562500007 ✔
3.0 | 2.0 | 1.0 | 2.0 |  1 |   -0.250000000 |   -0.250000020 ✔
3.0 | 2.0 | 1.0 | 2.0 |  2 |   -0.062500000 |   -0.062500019 ✔
3.0 | 2.0 | 1.0 | 2.7 |  0 |   -0.304504387 |   -0.304504391 ✔
3.0 | 2.0 | 1.0 | 2.7 |  1 |   -0.135335283 |   -0.135335310 ✔
3.0 | 2.0 | 1.0 | 2.7 |  2 |   -0.033833821 |   -0.033833829 ✔
3.0 | 2.0 | 2.0 | 1.0 |  0 |   -9.000000000 |   -9.000000464 ✔
3.0 | 2.0 | 2.0 | 1.0 |  1 |   -4.000000000 |   -4.000001333 ✔
3.0 | 2.0 | 2.0 | 1.0 |  2 |   -1.000000000 |   -1.000001338 ✔
3.0 | 2.0 | 2.0 | 2.0 |  0 |   -2.250000000 |   -2.250000029 ✔
3.0 | 2.0 | 2.0 | 2.0 |  1 |   -1.000000000 |   -1.000000083 ✔
3.0 | 2.0 | 2.0 | 2.0 |  2 |   -0.250000000 |   -0.250000076 ✔
3.0 | 2.0 | 2.0 | 2.7 |  0 |   -1.218017549 |   -1.218017558 ✔
3.0 | 2.0 | 2.0 | 2.7 |  1 |   -0.541341133 |   -0.541341157 ✔
3.0 | 2.0 | 2.0 | 2.7 |  2 |   -0.135335283 |   -0.135335316 ✔
3.0 | 2.0 | 2.7 | 1.0 |  0 |  -16.625376223 |  -16.625377080 ✔
3.0 | 2.0 | 2.7 | 1.0 |  1 |   -7.389056099 |   -7.389058562 ✔
3.0 | 2.0 | 2.7 | 1.0 |  2 |   -1.847264025 |   -1.847266500 ✔
3.0 | 2.0 | 2.7 | 2.0 |  0 |   -4.156344056 |   -4.156344109 ✔
3.0 | 2.0 | 2.7 | 2.0 |  1 |   -1.847264025 |   -1.847264179 ✔
3.0 | 2.0 | 2.7 | 2.0 |  2 |   -0.461816006 |   -0.461816146 ✔
3.0 | 2.0 | 2.7 | 2.7 |  0 |   -2.250000000 |   -2.250000016 ✔
3.0 | 2.0 | 2.7 | 2.7 |  1 |   -1.000000000 |   -1.000000045 ✔
3.0 | 2.0 | 2.7 | 2.7 |  2 |   -0.250000000 |   -0.250000061 ✔
3.0 | 2.7 | 1.0 | 1.0 |  0 |   -1.655457485 |   -1.655457571 ✔
3.0 | 2.7 | 1.0 | 1.0 |  1 |   -0.735758882 |   -0.735759128 ✔
3.0 | 2.7 | 1.0 | 1.0 |  2 |   -0.183939721 |   -0.183939966 ✔
3.0 | 2.7 | 1.0 | 2.0 |  0 |   -0.413864371 |   -0.413864377 ✔
3.0 | 2.7 | 1.0 | 2.0 |  1 |   -0.183939721 |   -0.183939735 ✔
3.0 | 2.7 | 1.0 | 2.0 |  2 |   -0.045984930 |   -0.045984944 ✔
3.0 | 2.7 | 1.0 | 2.7 |  0 |   -0.224041808 |   -0.224041810 ✔
3.0 | 2.7 | 1.0 | 2.7 |  1 |   -0.099574137 |   -0.099574156 ✔
3.0 | 2.7 | 1.0 | 2.7 |  2 |   -0.024893534 |   -0.024893540 ✔
3.0 | 2.7 | 2.0 | 1.0 |  0 |   -6.621829941 |   -6.621830283 ✔
3.0 | 2.7 | 2.0 | 1.0 |  1 |   -2.943035529 |   -2.943036510 ✔
3.0 | 2.7 | 2.0 | 1.0 |  2 |   -0.735758882 |   -0.735759867 ✔
3.0 | 2.7 | 2.0 | 2.0 |  0 |   -1.655457485 |   -1.655457507 ✔
3.0 | 2.7 | 2.0 | 2.0 |  1 |   -0.735758882 |   -0.735758944 ✔
3.0 | 2.7 | 2.0 | 2.0 |  2 |   -0.183939721 |   -0.183939776 ✔
3.0 | 2.7 | 2.0 | 2.7 |  0 |   -0.896167231 |   -0.896167239 ✔
3.0 | 2.7 | 2.0 | 2.7 |  1 |   -0.398296547 |   -0.398296565 ✔
3.0 | 2.7 | 2.0 | 2.7 |  2 |   -0.099574137 |   -0.099574161 ✔
3.0 | 2.7 | 2.7 | 1.0 |  0 |  -12.232268228 |  -12.232268859 ✔
3.0 | 2.7 | 2.7 | 1.0 |  1 |   -5.436563657 |   -5.436565469 ✔
3.0 | 2.7 | 2.7 | 1.0 |  2 |   -1.359140914 |   -1.359142736 ✔
3.0 | 2.7 | 2.7 | 2.0 |  0 |   -3.058067057 |   -3.058067096 ✔
3.0 | 2.7 | 2.7 | 2.0 |  1 |   -1.359140914 |   -1.359141028 ✔
3.0 | 2.7 | 2.7 | 2.0 |  2 |   -0.339785229 |   -0.339785331 ✔
3.0 | 2.7 | 2.7 | 2.7 |  0 |   -1.655457485 |   -1.655457497 ✔
3.0 | 2.7 | 2.7 | 2.7 |  1 |   -0.735758882 |   -0.735758916 ✔
3.0 | 2.7 | 2.7 | 2.7 |  2 |   -0.183939721 |   -0.183939765 ✔

Recurrence Relation between $E_{n+1}$ and $E_n$

\[\begin{equation} \left\{ \, \begin{aligned} 0 < \Delta E && 0 \leq n \leq n_\mathrm{max} \\ \Delta E < 0 && \mathrm{otherwise} \end{aligned} \right. \end{equation}\]

\[\Delta E = E_{n+1} - E_n\]

\[n_\mathrm{max} = \left\lfloor \lambda \right\rfloor - 1\]

PT = Antique.PoschlTeller(λ=2, m=1.0, ħ=1.0, x₀=1.0)
 n  Eₙ          ΔE
 0  -2.000000  +1.500000  0 < ΔE  ✔
 1  -0.500000  +0.500000  0 < ΔE  ✔
-----------------------------  nₘₐₓ(PT) = 1
 2  -0.000000  -0.500000  ΔE < 0  ✔
 3  -0.500000  -1.500000  ΔE < 0  ✔
 4  -2.000000  -2.500000  ΔE < 0  ✔
 5  -4.500000  -3.500000  ΔE < 0  ✔
 6  -8.000000  -4.500000  ΔE < 0  ✔

PT = Antique.PoschlTeller(λ=3, m=1.0, ħ=1.0, x₀=1.0)
 n  Eₙ          ΔE
 0  -4.500000  +2.500000  0 < ΔE  ✔
 1  -2.000000  +1.500000  0 < ΔE  ✔
 2  -0.500000  +0.500000  0 < ΔE  ✔
-----------------------------  nₘₐₓ(PT) = 2
 3  -0.000000  -0.500000  ΔE < 0  ✔
 4  -0.500000  -1.500000  ΔE < 0  ✔
 5  -2.000000  -2.500000  ΔE < 0  ✔
 6  -4.500000  -3.500000  ΔE < 0  ✔
 7  -8.000000  -4.500000  ΔE < 0  ✔

PT = Antique.PoschlTeller(λ=4, m=1.0, ħ=1.0, x₀=1.0)
 n  Eₙ          ΔE
 0  -8.000000  +3.500000  0 < ΔE  ✔
 1  -4.500000  +2.500000  0 < ΔE  ✔
 2  -2.000000  +1.500000  0 < ΔE  ✔
 3  -0.500000  +0.500000  0 < ΔE  ✔
-----------------------------  nₘₐₓ(PT) = 3
 4  -0.000000  -0.500000  ΔE < 0  ✔
 5  -0.500000  -1.500000  ΔE < 0  ✔
 6  -2.000000  -2.500000  ΔE < 0  ✔
 7  -4.500000  -3.500000  ΔE < 0  ✔
 8  -8.000000  -4.500000  ΔE < 0  ✔

PT = Antique.PoschlTeller(λ=10, m=1.0, ħ=1.0, x₀=1.0)
 n  Eₙ          ΔE
 0  -50.000000  +9.500000  0 < ΔE  ✔
 1  -40.500000  +8.500000  0 < ΔE  ✔
 2  -32.000000  +7.500000  0 < ΔE  ✔
 3  -24.500000  +6.500000  0 < ΔE  ✔
 4  -18.000000  +5.500000  0 < ΔE  ✔
 5  -12.500000  +4.500000  0 < ΔE  ✔
 6  -8.000000  +3.500000  0 < ΔE  ✔
 7  -4.500000  +2.500000  0 < ΔE  ✔
 8  -2.000000  +1.500000  0 < ΔE  ✔
 9  -0.500000  +0.500000  0 < ΔE  ✔
-----------------------------  nₘₐₓ(PT) = 9
10  -0.000000  -0.500000  ΔE < 0  ✔
11  -0.500000  -1.500000  ΔE < 0  ✔
12  -2.000000  -2.500000  ΔE < 0  ✔
13  -4.500000  -3.500000  ΔE < 0  ✔
14  -8.000000  -4.500000  ΔE < 0  ✔